Cómo verificar si un número es primo en Python

Este tutorial le enseñará cómo escribir un programa en Python para verificar si un el numero es primo o no.

Si alguna vez has realizado pruebas de codificación, te habrás topado con la cuestión matemática de la prueba de primalidad o para comprobar si un número es primo. Y en los próximos minutos aprenderá cómo encontrar la solución óptima a esta pregunta.

En este tutorial, usted:

• repasar los conceptos básicos de los números primos,
• escribir código Python para verificar si un número es primo, y
• optimícelo aún más para obtener un algoritmo de tiempo de ejecución O(√n).

Por todo esto y más, empecemos.

¿Qué es un número primo?

Comencemos repasando los conceptos básicos de los números primos.

En teoría de números, un número natural no ellos dicen principal si la exactamente dos factores: 1 y el número en sí (no). Recordatorio de tus matemáticas escolares: un número yo se dice que es un factor del número noSi yo Separar no uniformemente ✅

La siguiente tabla enumera algunos números, todos sus factores y si son primos.

no	factores	es premier?
1	1	No
2	1, 2	Sí
3	1, 3	Sí
4	1, 2, 4	No
7	1, 7	Sí
15	1, 3, 5, 15	No

De la tabla anterior, podemos señalar lo siguiente:

• 2 es el número primo más pequeño.
• 1 es un divisor de cualquier número.
• cada numero n es un factor en sí mismo.

Entonces 1 y n son factores triviales para cualquier número n. Y un número primo no debe tener otros factores que estos dos.

Esto significa que cuando pasas de 2 a n – 1, tienes que no para poder encontrar un factor no trivial que divida a n sin resto.

Algoritmo O (n) para verificar si un número es primo en Python

En esta sección, formalicemos el enfoque anterior en una función de Python.

Puede recorrer todos los números del 2 al n – 1 usando el range() objeto en Python.

en Python, range(start, stop, step) devuelve un objeto de rango. Luego puede recorrer el objeto de rango para obtener una secuencia de start todo el camino hasta stop -1 en etapas de step.

Como necesitamos el conjunto de enteros de 2 a n-1, podemos especificar range(2, n) y usarlo junto con for círculo.

Esto es lo que nos gustaría hacer:

• Si encuentras un número que divide no uniformemente sin resto, puede concluir inmediatamente que el número no es primo.

• Si ha pasado por todo el rango de números de 2 todo el camino hasta n-1 sin encontrar un número que divida no uniformemente, entonces el número es primo.

Función de Python para comprobar el número primo

Usando lo anterior podemos seguir adelante y definir la función is_prime() como sigue.

def is_prime(n):
  for i in range(2,n):
    if (n%i) == 0:
      return False
  return True

Ahora analicemos la definición de la función anterior.

• La función de arriba is_prime() toma un entero positivo no como argumento.
• Si encuentra un factor dentro del rango especificado de (2, n-1), la función devuelve False– porque el número no es primo.
• y vuelve True si recorre todo el circuito sin encontrar un cartero.

Luego, llamemos a la función con argumentos y verifiquemos si la salida es correcta.

is_prime(2)
# True

is_prime(8)
# False

is_prime(9)
# False

is_prime(11)
# True

En el resultado de arriba, ves que 2 y 11 son primos (la función devuelve True). Y 8 y 9 no son primos (la función devuelve False).

Cómo optimizar la función Python is_prime()

Podemos hacer una pequeña optimización aquí. Mire la lista de factores en la siguiente tabla.

Número	factores
6	1, 2, 36
diez	1, 2, 5diez
18	1, 2, 3, 6, 918

Bueno, podemos ver que el único factor de no que es mayor que n/2 es no él mismo.

Eso significa que no necesita hacer un bucle hasta n – 1. En su lugar, puede ejecutar el bucle solo hasta n/2.

Si no puede encontrar un factor no trivial antes de n/2, tampoco puede encontrar uno más allá de n/2.

Ahora vamos a modificar la función. is_prime() para verificar factores en el rango (2, n/2)

def is_prime(n):
  for i in range(2,int(n/2)):
    if (n%i) == 0:
      return False
  return True

Avancemos y verifiquemos la salida a través de algunas llamadas a funciones.

is_prime(9)
# False

is_prime(11)
# True

Aunque pueda parecer que lo hemos optimizado, este algoritmo no es más eficiente que el anterior en cuanto a complejidad de ejecución. De hecho, ambos tienen Seguro) complejidad de ejecución: proporcional al valor de n o lineal en n.

¿Podemos hacerlo mejor? ¡Sí, podemos!

▶️ Continúe con la siguiente sección para determinar cómo mejorar la complejidad temporal de las pruebas de números primos.

Algoritmo O(√n) para verificar el número primo en Python

A veces los factores de un número aparecen en pares.

Sí un es un factor del número noentonces también hay un factor b tal que axb=no simplemente, ab=n.

Comprobemos esto a través de un ejemplo.

La siguiente tabla muestra los factores del número 18 que aparecen en pares. Puede verificar lo mismo para algunos números más si lo desea.

También tenga en cuenta que √18 es aproximadamente 4,24.

Y en factores que ocurren en pares (una B)puedes ver que si un es menor que 4.24, entonces b es mayor que 4.24 – en este ejemplo, (2, 18) y (3, 6).

La siguiente figura muestra los factores de 18 trazados en la recta numérica.

cryptoshitcompra.com/wp-content/uploads/2022/05/Como-verificar-si-un-numero-es-primo-en-Python.png» alt=»carteros de línea digital» class=»wp-image-88949″/>

Si el número n es un cuadrado perfecto, tendrás a = b = √n como uno de los factores.

▶️ Mira los factores de 36 en la siguiente tabla. Como 36 es un cuadrado perfecto, a = b = 6 es uno de los factores. Para todos los demás pares de factores (a, b), a < 6 et b > 6 son válidos.

En resumen, tenemos lo siguiente:

• cada numero no Se puede escribir como n = axb
• Sí no es un cuadrado perfecto, entonces a = segundo = √n.
• Y si un < segundoentonces, un < √n y b > n.
• De lo contrario, si a > bentonces a > √n y segundo < √n.

Entonces, en lugar de iterar a través de todos los enteros hasta n/2, puede optar por ejecutar hasta √n. Y es mucho más eficiente que nuestro enfoque anterior.

Cómo cambiar el algoritmo is_prime() a O(√n)

Sigamos optimizando la función para buscar números primos en Python.

import math
def is_prime(n):
  for i in range(2,int(math.sqrt(n))+1):
    if (n%i) == 0:
      return False
  return True

Ahora, analicemos la definición de la función anterior:

• Para calcular la raíz cuadrada de un número, importemos el módulo matemático incorporado de Python y usemos math.sqrt() Una función.
• Me gusta no puede que no sea un cuadrado perfecto, tendremos que convertirlo en un número entero. Usar int(var) tirar var en un int.
• Para asegurarnos de que realmente verificamos hasta √n, agregamos un más uno como range() La función excluye el punto final del rango predeterminado.

La siguiente celda de código verifica que nuestra función is_prime() funciona correctamente.

is_prime(8)
# False

is_prime(15)
# False

is_prime(23)
# True

En la siguiente sección, vamos a crear algunos gráficos simples para entender O(n) y O(√n) visualmente.

Compare visualmente O(n) y O(√n)

▶️ Ejecute el siguiente fragmento de código en un entorno de cuaderno Jupyter de su elección.

import numpy as np
import seaborn as sns
import pandas as pd


n = 20

x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)

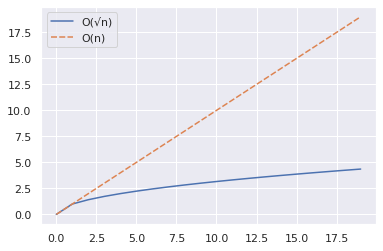
El fragmento anterior muestra cómo puede trazar las curvas para n y √n para un rango de valores.

• Usamos la función NumPy arange() para crear una matriz de números.
• Y luego recopilamos los valores de n y √n hasta 20 inclusive, en un Marco de datos de pandas.
• Luego graficamos usando diagrama de línea de seaborn () Una función.

En el siguiente gráfico, vemos que √n es significativamente menor que n.

Ahora aumentemos el rango a 2000 y repitamos los mismos pasos que arriba.

import numpy as np
import seaborn as sns
import pandas as pd


n = 2000

x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)

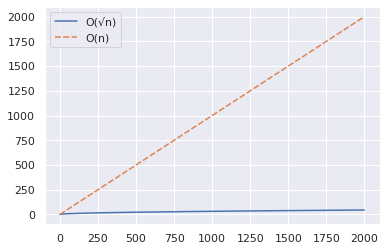
Del gráfico anterior, puedes deducir que el algoritmo O(√n) es significativamente más rápido cuando se prueba si un número grande es primo.

Aquí hay un ejemplo rápido: 2377 es un número primo, ¡compruébalo! 😀

Mientras que el enfoque O(n) tomará el orden de 2000 pasos, el algoritmo O(√n) puede ayudar a llegar a la respuesta en solo 49 pasos.✅

Conclusión

⏳ Y llega el momento del pequeño resumen.

• Para verificar si un número es primo, el enfoque ingenuo es iterar a través de todos los números en el rango (2, n-1). Si no puede encontrar un factor que divida a n, entonces n es primo.
• Dado que el único factor de n mayor que n/2 es n mismo, puede optar por ejecutar solo hasta n/2.
• Ambos enfoques anteriores tienen una complejidad de tiempo de O(n).
• Dado que los factores de un número aparecen en pares, solo puedes correr hasta √n. Este algoritmo es mucho más rápido que O(n). Y la ganancia es significativa al comprobar si un número grande es primo o no.

Espero que entienda cómo verificar si un número es primo en Python. Como siguiente paso, puede consultar nuestro Tutorial de programas Python de operaciones de cadenas, donde aprenderá cómo verificar si las cadenas son palíndromos, anagramas, etc.

Nos vemos en otro tutorial. Hasta entonces, ¡feliz codificación! 👩🏽‍💻