Un tutorial para codificar entrevistas.

Ordenar listas de datos es una parte crucial del procesamiento en aplicaciones.

Es útil para mostrar datos y realizar búsquedas. Por eso no sorprende que todo buen ingeniero de software sepa cómo ordenar tablas. Este artículo explica algunos de los algoritmos más comunes para ordenar matrices en JavaScript.

¿Qué es ordenar y por qué es útil?

La clasificación es la organización sistemática de valores según un orden determinado. Este orden puede ser descendente o ascendente. Ordenar tablas en JavaScript es útil porque permite que los datos se muestren de una manera más significativa.

Por ejemplo, es posible que una persona desee ver los archivos ordenados primero y los archivos más recientes o los productos ordenados por precio. También es útil para realizar una búsqueda binaria de datos, que sólo funciona con datos ordenados.

Si bien existen funciones y bibliotecas que le ayudarán a ordenar datos fácilmente, aún necesita saber cómo funciona la clasificación entre bastidores para codificar entrevistas o cuándo necesita escribir código de bajo nivel.

Algoritmos de clasificación de matrices de JavaScript

Ordenamiento de burbuja

cryptoshitcompra.com/wp-content/uploads/2023/09/Un-tutorial-para-codificar-entrevistas.jpg»/>

Bubble Sort es posiblemente el algoritmo más sencillo de entender e implementar. Funciona atravesando la matriz en una sola pasada. En cada pasada, recorremos la matriz, de principio a fin, comparando dos elementos adyacentes. Si los artículos están en el orden incorrecto, los cambiamos.

Realizamos n pases donde n es el número de elementos de la matriz. En cada pasada, la tabla se ordena empezando por la derecha. El pseudocódigo del algoritmo para ordenar números en orden ascendente es el siguiente:

1. Let n be the number of elements in the array
2. Loop n times, keeping count of the loops using i (doing the following in each loop)
   a. loop the array from the second element to the (n - i)th element
   b. if the previous element is greater than the current element, swap them.

Traduciéndolo a JavaScript, el código se vería así:

function sort(arr) {
    const n = arr.length;

    for (let i = 0; i < n; i++) {
        for (let j = 1; j < n - i; j++) {
            if (arr[j - 1] &gt; arr[j]) {
                const temp = arr[j - 1];
                arr[j - 1] = arr[j];
                arr[j] = temp;
            }
        }
    }
    
    return arr;
}

Para comprender mejor lo que está sucediendo, recomendaría agregar un archivo console.logs dentro de ambos bucles para ver cómo cambia la tabla con cada pasada.

En el código siguiente, modifiqué la función de clasificación para agregar console.logs dentro de ambos bucles. También creé una pequeña matriz sin clasificar que ordené usando la función de clasificación.

function sort(arr) {
    const n = arr.length;

    for (let i = 0; i < n; i++) {
	console.log(`Pass: ${i}`);

        for (let j = 1; j < n - i; j++) {
            if (arr[j - 1] &gt; arr[j]) {
                const temp = arr[j - 1];
                arr[j - 1] = arr[j];
                arr[j] = temp;
            }
	
	    console.log(arr);
        }
    }
    
    return arr;
}

const array = [9, 2, 7, 4, 1];
sort(array);

console.log(array);

El resultado de ejecutar el código anterior sería:

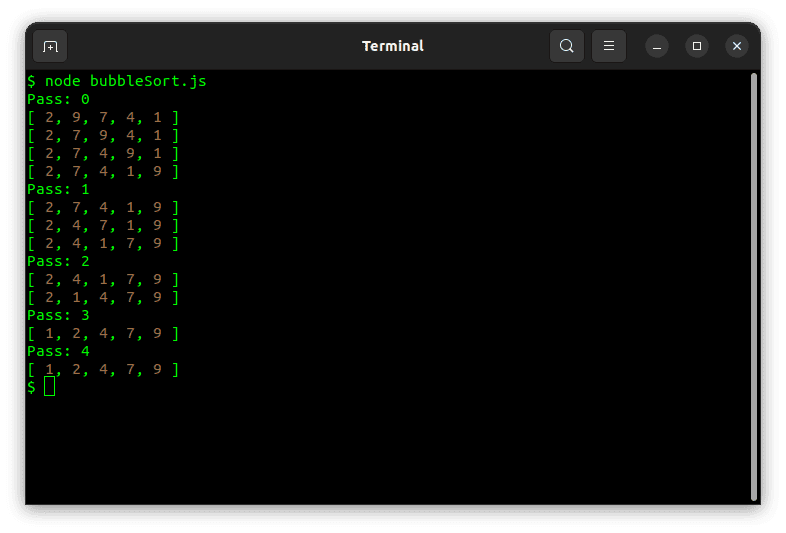
La clasificación de burbujas tiene una complejidad temporal Big O de O (n ^ 2). En efecto, realiza n pasadas, que atraviesan la matriz en cada pasada. Por tanto, no se adapta bien. Sin embargo, tiene una complejidad espacial de O(1) ya que modifica los elementos de la matriz en su lugar.

Tipo de inserción

La ordenación por inserción es un algoritmo popular de ordenación de matrices de JavaScript. Supongamos que usamos la ordenación por inserción para ordenar los valores en orden ascendente. El algoritmo funciona eligiendo un número, al que llamaremos num. Luego mueve num hacia la izquierda hasta que cada segundo número a la izquierda de num sea menor que num. Todos los números se ordenarán si se hace desde el segundo elemento hasta el final. Aquí hay una descripción en pseudocódigo.

1. Let n be the number of elements in the array
2. Loop i from 1 to n - 1 (start from the second element)
    a. Set currentElement to array[i]
    b. Set j to i - 1
    c. While j >= 0 and array[j] > current_element
       i. Move array[j] to array[j+1]
       ii. Decrement j by 1
    d. Set array[j+1] to current_element

Y ahora el pseudocódigo implementado en JavaScript es el siguiente.

function insertionSort(array) {
  const n = array.length;

  for (let i = 1; i < n; i++) {
    const currentElement = array[i];
    let j = i - 1;

    while (j >= 0 && array[j] > currentElement) {
      array[j + 1] = array[j];
      j -= 1;
    }

    array[j + 1] = currentElement;
  }

  return array;
}

En cuanto a Bubble Sort, agregar console.logs te ayuda a visualizar lo que está sucediendo. El siguiente fragmento de código muestra la ordenación por inserción en funcionamiento.

function sort(array) {
    const n = array.length;

    for (let i = 1; i < n; i++) {
        const currentElement = array[i];
        let j = i - 1;
        console.log("Placing element:", currentElement);

        while (j >= 0 && array[j] > currentElement) {
            array[j + 1] = array[j];
            j -= 1;
        }

        array[j + 1] = currentElement;
        console.log("Placed it at position:", j + 1);
        console.log(array);
    }

    return array;
}

const array = [4, 1, 2, 5, 3];
sort(array);

Y al ejecutar el fragmento anterior se obtiene el siguiente resultado:

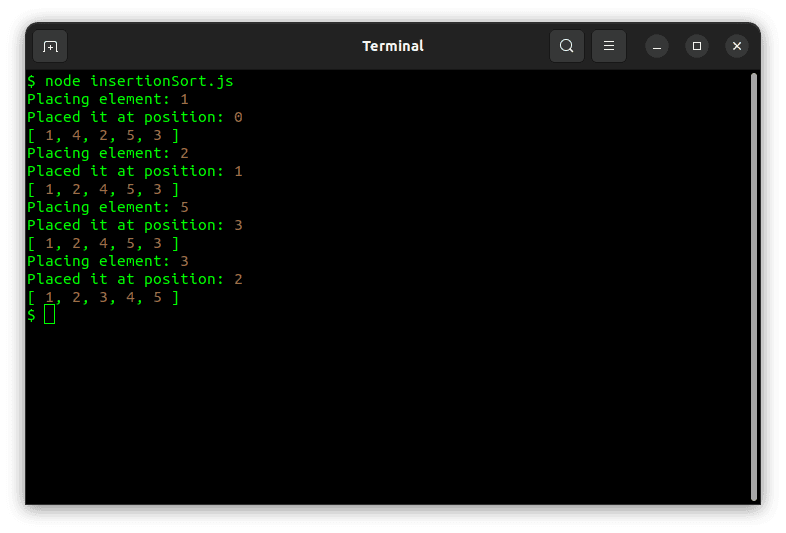
Combinar ordenar

Mientras que la ordenación por inserción y la ordenación por burbuja evolucionan en tiempo cuadrático, la ordenación por fusión evoluciona en tiempo casi lineal. Tiene una complejidad temporal de O (n * log (n)).

La clasificación por combinación utiliza la estrategia de dividir y conquistar. La matriz se divide repetidamente en matrices más pequeñas de 1 elemento cada una. Después de la división, se fusionan.

La división es recursiva por lo que la matriz se puede volver a ensamblar más tarde.

Al fusionar la tabla, los subarreglos se fusionan en orden. La fusión se realiza de la misma manera que fusionaría una matriz ordenada. El pseudocódigo para hacer esto se escribe a continuación:

1. If the length of the array is 1 or less, return the array (base case)
2. Find the middle index:
   a. Set mid to the floor of (length of the array / 2)
3. Divide the array into two subarrays:
   a. Create leftArray and copy the first half of the array into it (from index 0 to mid)
   b. Create rightArray and copy the second half of the array into it (from index mid+1 to the end)
4. Recursively call MergeSort on leftArray
5. Recursively call MergeSort on rightArray
6. Merge the two sorted subarrays:
   a. Create an empty resultArray
   b. While both leftArray and rightArray are not empty:
      i. If the first element in leftArray is less than or equal to the first element in rightArray, append it to resultArray
      ii. Otherwise, append the first element in rightArray to resultArray
   c. Append any remaining elements in leftArray to resultArray (if any)
   d. Append any remaining elements in rightArray to resultArray (if any)
7. Return resultArray

Implementarlo en JavaScript daría como resultado lo siguiente:

function sort(array) {

	// Base case in which we stop subdividing the array
	if (array.length == 1) {
		return array;
	}

	// Finding the middle point of the array
	const m = Math.round(array.length / 2);

	// Divide the array into two halves
	const leftUnsorted = array.slice(0, m);
	const rightUnsorted = array.slice(m);

	// Recursively call merge sort
	const leftSorted = sort(leftUnsorted);
	const rightSorted = sort(rightUnsorted);

	// Return a merged sorted array
	return merge(leftSorted, rightSorted);
}

function merge(left, right) {
	// Merge two sorted lists
	let result = [];
	let leftIndex = 0;
	let rightIndex = 0;

	while (leftIndex < left.length && rightIndex < right.length) {
		if (left[leftIndex] < right[rightIndex]) {
			result.push(left[leftIndex]);
			leftIndex += 1;
		} else {
			result.push(right[rightIndex]);
			rightIndex += 1;
		}
	}

	return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}

Si ejecuta el código con una tabla de muestra, debería funcionar.

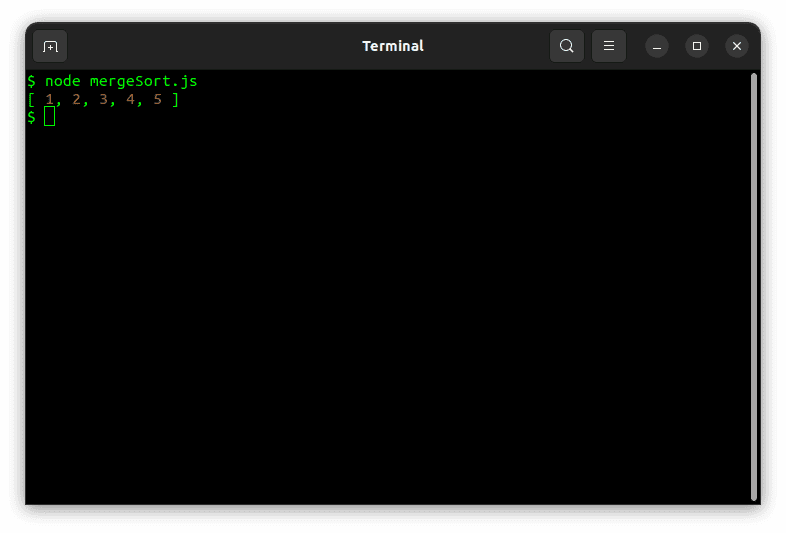
Ordenación rápida

Al igual que Merge Sort, Quick Sort se basa en la estrategia de dividir y conquistar. El algoritmo selecciona un elemento pivote. Luego mueve todos los elementos más grandes que el pivote hacia su derecha y más pequeños que el pivote hacia su izquierda. Una vez hecho esto, el pivote estará en la posición correcta.

Para mover elementos alrededor del pivote, el algoritmo comienza moviendo el pivote hasta el final de la matriz.

Después de moverlo, usamos un puntero para recorrer desde la izquierda de la matriz, buscando el primer número mayor que el pivote. Simultáneamente, usamos otro bucle de puntero desde la derecha de la matriz, buscando el primer número debajo del pivote. Una vez identificados los dos números, los intercambiamos. Este procedimiento se repite hasta que el puntero izquierdo sea más grande que el puntero derecho.

Cuando nos detenemos, intercambiamos el mayor de los dos últimos números intercambiados con el pivote. En este punto el pivote estará en la posición correcta; Los números debajo del pivote estarán a la izquierda, mientras que los de arriba estarán a la derecha.

Este procedimiento se repite de forma recursiva para los subarreglos a la izquierda y a la derecha del pivote hasta que solo quede un elemento en los subarreglos.

Aquí está el pseudocódigo para una clasificación rápida:

1. If lessThanPointer is less than greaterThanPointer:
    a. Choose a pivot element from the array
    b. Move elements such that elements less are to the left and elements greater are to the right:
    c. Recursively call Quicksort on leftSubarray
    d. Recursively call Quicksort on rightSubarray

Y convirtiéndolo a JavaScript:

function sort(array, low, high) {
    if (low < high) {
        // Choose the pivot index and partition the array
        const pivotIndex = move(array, low, high);

        // Recursively sort the subarrays to the left and right of the pivot
        sort(array, low, pivotIndex - 1);
        sort(array, pivotIndex + 1, high);
    }
}

function move(array, low, high) {
    // Select the pivot element (in this case, the last element)
    const pivotElement = array[high];

    // Initialize the index for the smaller element
    let i = low - 1;

    for (let j = low; j < high; j++) {
        // If the current element is less than or equal to the pivot, swap it with the element at index i+1
        if (array[j] <= pivotElement) {
            i += 1;
            const temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
    }

    // Swap the pivot element into its correct position
    const temp = array[i];
    array[i] = array[j];
    array[j] = temp;

    // Return the index of the pivot element
    return i + 1;
}

Ordenar una tabla de muestra con Quick Sort en Node.js debería dar como resultado lo siguiente:

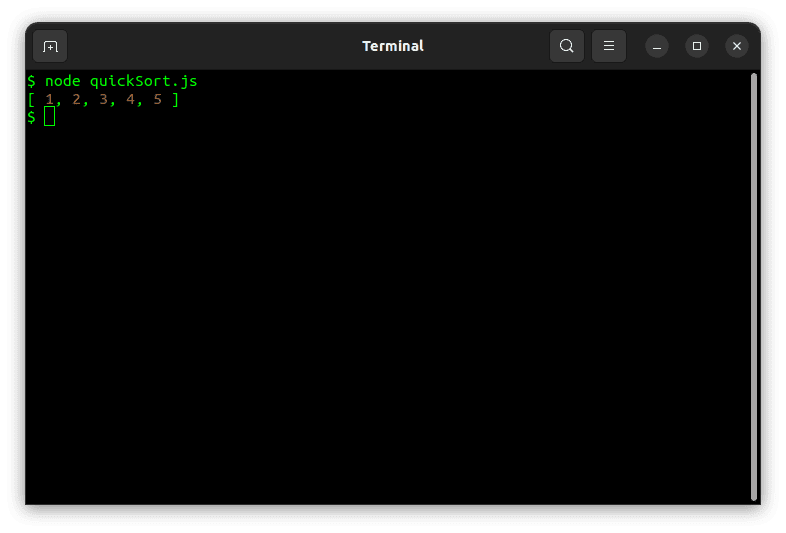
En el mejor de los casos, Quicksort se ejecuta en una complejidad de tiempo casi lineal. El uso de espacio en Quick Sort también aumenta de forma logarítmica. Por lo tanto, es relativamente eficiente en comparación con otros algoritmos de clasificación de matrices de JavaScript.

Consejos para sus entrevistas de codificación

❇️La práctica es clave. Le ayuda a aprender diferentes algoritmos, pero lo más importante es que le ayuda a desarrollar habilidades de resolución de problemas y pensamiento computacional. También puedes practicar en plataformas como Código Leet Y AlgoExperto.

❇️ Intente solucionar el problema primero. En lugar de saltar directamente a la solución, intente resolverla, ya que esto le ayudará a desarrollar sus habilidades para resolver problemas.

❇️ Si un problema tarda demasiado, salte directamente a la solución; siempre puedes aprender cómo resolver el problema a partir de la solución. La mayoría de las plataformas de aprendizaje ofrecen soluciones. ChatGPT o Google Bard también son útiles para explicar conceptos.

❇️ Además, no escriba código inmediatamente; Escriba sus soluciones en una pizarra y piense en ellas antes de escribir código. El pseudocódigo también es una forma útil de escribir ideas rápidamente.

Conclusión

En este artículo, cubrimos los algoritmos de clasificación más populares. Sin embargo, aprender todo esto puede parecer abrumador al principio. Por lo tanto, generalmente recomiendo mezclar diferentes fuentes en lugar de depender de una sola. ¡Feliz codificación!

A continuación, aprenda a comprender la función ordenada en Python.