¿Cómo crear matrices de números espaciados uniformemente en Python?

Este tutorial le enseñará cómo usar NumPy espacio lineal() para crear una matriz de números espaciados uniformemente en Python.

Aprenderás la sintaxis de NumPy linspace()seguido de ejemplos que le ayudarán a entender cómo usarlo.

Notar: Para seguir este tutorial, debe tener Python y NumPy instalados.

¿Aún no tienes NumPy? Hemos preparado una guía de instalación rápida para usted.

¡Empecemos!

Instalar e importar NumPy

Antes de comenzar el tutorial, repasemos rápidamente los pasos para instalar la biblioteca NumPy.

⏩ Si ya ha instalado NumPy, no dude en pasar a la siguiente sección.

• Si está utilizando Google Colab, un entorno de notebook Jupyter basado en la nube, puede importar NumPy y comenzar a codificar de inmediato. (recomendado para este tutorial ✅)
• Si desea configurar un entorno de trabajo local, le recomiendo instalar la distribución Anaconda de Python. Anaconda viene con varios paquetes útiles preinstalados. Puede descargar el instalador para su sistema operativo. El proceso de instalación solo toma unos minutos.⌛
• Si Python ya está instalado en su computadora, aún puede instalar la distribución de Anaconda. Puede usar conda o pip para instalar y administrar paquetes. Puede ejecutar uno de los siguientes comandos desde el símbolo del sistema de Anaconda para instalar NumPy.

# Install NumPy using conda
conda install numpy

# Install NumPy using pip
pip install numpy

En un siguiente paso, importe numpy bajo el seudónimo np ejecutando el siguiente comando. Esto lo ayudará a hacer referencia a NumPy como np— sin tener que teclear numpy cada vez que accede a un elemento del módulo.

import numpy as np

En el futuro, usaremos la notación de puntos para acceder a todas las funciones de la biblioteca NumPy de esta manera: np.<func-name&gt;.

El caso de los números regularmente espaciados

Cuando trabaje con matrices NumPy, a veces necesitará crear una matriz de números espaciados uniformemente en un intervalo.

Antes de continuar, repasemos rápidamente otra función similar np.arange().

NumPy linspace() vs NumPy arange()

Si alguna vez ha usado NumPy, probablemente habría usado np.arange() para crear una matriz de números en un rango específico.

Lo sabes np.arange(start, stop, step) devuelve una matriz de números de start hasta pero sin incluir stopen etapas de step; el tamaño de paso predeterminado es 1.

Sin embargo, el valor de paso no siempre puede ser obvio. Veamos por qué este es el caso.

Por ejemplo, si necesita 4 números espaciados uniformemente entre 0 y 1, sabe que el tamaño del paso debe ser 0,25. pero si usas np.arange()no incluye el valor de parada de 1, por lo que deberá elegir un intervalo que supere el valor de parada.

La siguiente imagen ilustra algunos ejemplos más en los que necesita una cantidad específica de puntos espaciados uniformemente en el intervalo [a, b].

cryptoshitcompra.com/wp-content/uploads/2022/04/¿Como-crear-matrices-de-numeros-espaciados-uniformemente-en-Python.png» alt=»numpy-linspace» class=»wp-image-86863″/>

Nuestro primer ejemplo de 4 puntos espaciados uniformemente en [0,1] fue bastante fácil. Sabes que el tamaño del paso entre los puntos debe ser 0,25.

Suponga que tiene un ejemplo un poco más complicado, donde necesita enumerar 7 puntos espaciados uniformemente entre 1 y 33. Aquí, el tamaño del paso puede no ser claro de inmediato. Sin embargo, puede determinar manualmente el valor de step en este caso.

Sin embargo, np.linspace() está aquí para hacer su trabajo aún más fácil! 😄

png» alt=»use-numpy-linspace» class=»wp-image-86864″/>

Cuando usas np.linspace(), solo necesita especificar el número de puntos en el intervalo, sin preocuparse por el tamaño del paso. Y recuperará la matriz como desee.

Con esta motivación sigamos aprendiendo la sintaxis de NumPy linspace() en la siguiente sección.

Sintaxis de NumPy linspace()

La sintaxis para usar NumPy linspace() se muestra a continuación:

np.linspace(start, stop, num, endpoint, retstep, dtype, axis)

Inicialmente, la sintaxis anterior puede parecer muy complicada con muchos parámetros.

Sin embargo, la mayoría de ellos son Opcional parámetros, y llegaremos a una sintaxis mucho más simple en unos minutos.

Ahora comencemos analizando la sintaxis anterior:

• start y end son respectivamente los puntos inicial y final del intervalo. El inicio y el apagado pueden ser escalares o matrices. Nos limitaremos a valores escalares iniciales y finales en este tutorial.
• num es el número de puntos espaciados uniformemente. Y es un parámetro opcional con un valor predeterminado de 50.
• endpoint también es un parámetro opcional que puede ser verdadero o falso.
• El valor predeterminado es Verdadero, lo que significa que el punto final se incluirá en el intervalo predeterminado. Sin embargo, puede establecerlo en False para excluir el punto final.
• retstep es otro parámetro opcional que toma valores booleanos verdaderos o falsos. Cuando se establece en True, se devuelve el valor del paso.
• dtype es el tipo de datos de los números en la matriz. El tipo generalmente se infiere como un flotante y no es necesario proporcionarlo explícitamente.
• axis es otro parámetro opcional que indica el eje a lo largo del cual se deben almacenar los números. Y esto sólo es relevante cuando el start y el stop los valores son en sí mismos matrices.

▶️ ¿Y qué? np.linspace() ¿Devolver a?

Devuelve una matriz N-dimensional de números espaciados uniformemente. Y si el parámetro retstep se establece en Truetambién devuelve el tamaño del paso.

Basado en la discusión hasta ahora, aquí hay una sintaxis simplificada para usar np.linspace():

np.linspace(start, stop, num)

La línea de código anterior devolverá una matriz de num números espaciados uniformemente en el intervalo [start, stop].

Ahora que conoce la sintaxis, comencemos a codificar ejemplos.

Cómo crear matrices espaciadas uniformemente con NumPy linspace()

#1. Como primer ejemplo, creemos una matriz de 20 números espaciados uniformemente en el intervalo [1, 5].

Puede especificar los valores de start, stopy num como argumentos de palabras clave. Esto se muestra en la siguiente celda de código:

import numpy as np
arr1 = np.linspace(start = 1,stop = 5,num = 20)
print(arr1)

# Output:
[1.         1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
 4.78947368 5.        ]

Observe cómo los números en la matriz comienzan en 1 y terminan en 5, incluidos ambos extremos. También observe cómo los números, incluidos los puntos 1 y 5, se representan como float en la matriz devuelta.

#2. En el ejemplo anterior, pasaste los valores de start, stopy num como argumentos de palabras clave. Si pasa los argumentos en el orden correcto, también podría usarlos como argumentos posicionales con sólo los valores, como se muestra a continuación.

import numpy as np
arr2 = np.linspace(1,5,20)
print(arr2)

# Output:
[1.         1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
 4.78947368 5.        ]

#3. Ahora vamos a crear otra matriz donde definimos retstep para True.

Esto significa que la función ahora devolverá tanto la matriz como el paso. Y podemos descomprimirlos en dos variables arr3: la matriz, y step_size: el tamaño de paso devuelto.

La siguiente celda de código explica cómo puede hacer esto.

import numpy as np
arr3, step_size = np.linspace(1,5,20,retstep = True)
print(arr3)

# Output:
[1.         1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
 4.78947368 5.        ]

# Output:
print(step_size)
0.21052631578947367

#4. Como último ejemplo, dejemos endpoint para Falsey comprobar lo que está sucediendo.

import numpy as np
arr4 = np.linspace(1,5,20,endpoint = False)
print(arr4)

# Output:
[1.  1.2 1.4 1.6 1.8 2.  2.2 2.4 2.6 2.8 3.  3.2 3.4 3.6 3.8 
4.  4.2 4.4 4.6 4.8]

En la matriz devuelta, puede ver que 1 está incluido, mientras que 5 no está incluido. Y el último valor en la matriz es 4.8, pero todavía tenemos 20 números.

Hasta ahora, solo hemos generado matrices de números espaciados uniformemente. En la siguiente sección, visualice trazando estos números.

Cómo graficar números espaciados uniformemente en un intervalo

En esta sección, elijamos [10,15] como el intervalo de interés. y luego usar np.linspace() para generar dos arreglos, cada uno con 8 y 12 puntos, respectivamente.

Una vez hecho esto, podemos usar la función de trazado del matplotlib biblioteca para graficarlos.

Para mayor claridad, exprimiremos las dos matrices de N1 = 8 y N2 = 12 puntos uniformemente espaciados en diferentes posiciones a lo largo del eje y.

El siguiente fragmento de código demuestra esto.

import numpy as np
import matplotlib.pyplot as plt

N1 = 8
N2 = 12

a = 10
b = 15

y1 = np.zeros(N1)
y2 = np.zeros(N2)

x1 = np.linspace(a, b, N1)
x2 = np.linspace(a, b, N2)

plt.plot(x1, y1-0.5, 'o')
plt.plot(x2, y2 + 0.5, 'o')

plt.ylim([-1, 1])

plt.title(f'Evenly Spaced Numbers in the Interval [{a},{b}]')
plt.xlabel('Interval')

plt.show()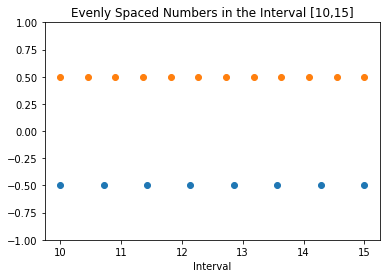

La generación de puntos espaciados uniformemente puede ser útil cuando se trabaja con funciones matemáticas. Aprenderemos más sobre esto en la siguiente sección.

Cómo usar NumPy linspace() con funciones matemáticas

Después de generar una matriz de números espaciados uniformemente usando np.linspace()puedes calcular los valores de las funciones matemáticas en el intervalo.

En la siguiente celda de código, primero genera 50 puntos espaciados uniformemente en el rango de 0 a 2π. Y luego crea la matriz. y utilizando np.sin() en la mesa x. Tenga en cuenta que puede omitir la num porque el valor por defecto es 50. Siempre lo usaremos de forma explícita.

Como siguiente paso, puede trazar la función seno en el intervalo [0, 2π]. Para hacer esto, puedes usar matplotlib, como en el ejemplo anterior. Más específicamente, el plot() función en matplotlib.pytplot se utiliza para crear un gráfico de líneas.

import numpy as np
import matplotlib.pyplot as plt

N = 50

a = 0.0
b = 2*np.pi

x = np.linspace(a, b, N)
y = np.sin(x)

plt.plot(x, y, marker = "o")

plt.ylim([-1, 1])
plt.title(f'y = sin(x)')
plt.xlabel('x ---->')

plt.show()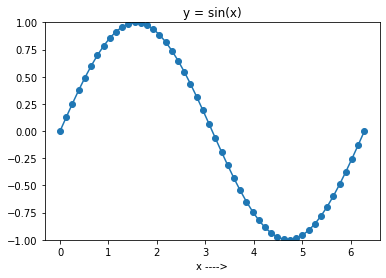

Ahora ejecute la configuración del código anterior N igual a 10. Obtendrá la gráfica como se muestra en la figura a continuación.

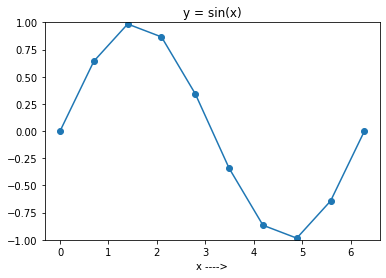
Y puede ver que la trama no es muy fluida, porque solo ha seleccionado 10 puntos en el intervalo.

En general, cuanto mayor sea el número de puntos que considere, más suave será el gráfico de la función.

Conclusión

Aquí hay un resumen de lo que aprendimos.

• np.linspace (inicio, parada, número) devuelve una matriz de número números espaciados uniformemente en el intervalo [start, stop].
• Establecer el parámetro opcional punto final para Falso excluir detenery establezca el intervalo en [comienza a parar)[comienza a parar][commencerarrêter)[startstop).
• Ajustar volver atrás para Real opcionalmente para obtener el tamaño del paso.
• Genere matrices espaciadas uniformemente usando np.linspace()luego use la matriz con funciones matemáticas.

Espero que ahora entiendas cómo np.linspace() obras. Puede optar por ejecutar los ejemplos anteriores en el cuaderno de Jupyter. Consulte nuestra guía sobre Jupyter Notebook u otras alternativas de Jupyter que pueda considerar.

Nos vemos pronto en otro tutorial de Python. Hasta entonces, ¡sigue programando! 😀